Attenzione! Se leggi questo messaggio significa cha hai disabilitato JavaScript

In tal caso le funzionalità del sito non sono disponibili.

 

Math

● Le espressioni si possono inserire solamente tramite la tastiera dell'app
● Il campo nel quale sarà inserita l'espressione è quello evidenziato in giallo
● Il campo in cui inserire l'espressione si seleziona semplicemente facendo click su di esso. Il campo diventerà così evidenziato in giallo
● Non è possibile comporre parole arbitrarie in quanto inserendo le lettere dell'alfabeto verrà inserito uno spazio dopo di essa per cui ogni lettera sarà riconosciuta come una variabile a se
● Inserendo le varie funzioni predefinite verrà inserito il suo nome e quando si cancella questo elemento verrà cancellato l'intero nome

Cancella l'intera espressione

Cancella l'ultima espressione inserita

Sposta il cursosre di un'espressione a sinistra

Sposta il cursosre di un'espressione a destra

Using the following buttons you can perform operations related to points in the cartesian plane

Distance between 2 points
Midpoint
Intersection of 2 curves
Barycenter
Circumcenter
Orthocenter

Input of the expressions

• The coordinates of the points are inserted as in the following example by separating the coordinates with the comma.

sqrt(3),a

• There is no need to type in the round brackets to enclose the coordinates
• The coordinates of the points can contain letters because the literal calculation is also performed

• Equations (straight lines and conics) can be inserted either explicitly or implicitly
• In the equations you can not enter parameters so only the letters x and y must appear
• The product between two letters can be indicated with an asterisk symbol (*) or by leaving a space between the letters. If you write two or more letters consecutively, it is not interpreted as a product but as a “single variable (x * y = product between x and y, x y = product between x and y; xy = single variable called xy)

Examples of calculation processes performed by the software (click on the image to see the related development):

You can test different input shapes by copying the text in red in the image captions and pasting it into the data entry window that appears by clicking any of the buttons at the top of the page to perform an operation (Distance between two points, Midpoint of a segment, etc …).

Examples of Inputs

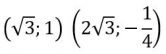
Points coordinates sqrt(3),1 2sqrt(3),-1/4

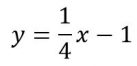
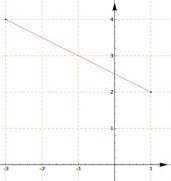
equation of a straight line in explicit form y=1/4x-1

Equation of the straight line in an implicit form
2x+sqrt(3)y-1=0

Equation of a conic (complete with second degree in x y)
x^2+x y-y^2-x=0

Equation of a parabola with axis parallel to the x axis
x=y^2-1

Examples of development carried out by the system (click on the image to see the related course):

DISTANCE BETWEEN TWO POINTS: The system uses the appropriate formula by checking whether the two points have common coordinates or not.

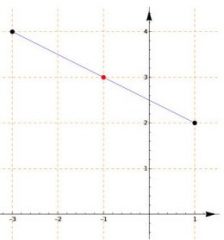
Medium Point: the system recognizes if the points have some co-ordination in common and in case adapts the application of the formulas to the data provided

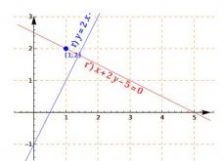
INTERSECTION BETWEEN TWO CURVES: The system constructs and solves the system formed by the equations of the two curves

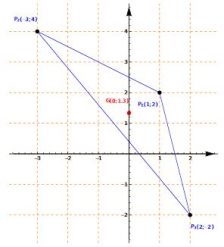
BARICENTER OF A TRIANGLE: The system directly applies the formula to determine the center of gravity

CIRCOCENT OF A TRIANGLE: The system calculates two axes of the triangle and intersects them to find the circumcentre

ORTOCENTRO OF A TRIANGLE: The system calculates two heights of the triangle and intersects them to find the orthocenter