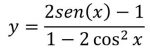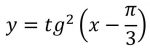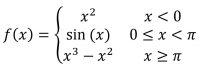Attenzione! Se leggi questo messaggio significa cha hai disabilitato JavaScript
In tal caso le funzionalità del sito non sono disponibili.




Complete study of a function
Through the following buttons you can perform a complete study of a function or have the individual parts of the study with more details
Complete study of a function
Study of the domain of a function
Study of the points of discontinuity of a function
Study of the sign of the first derivative
Examples of calculation processes performed by the software (click on the image to see the related development):
Do not enter “y =” but only the expression in x
You can test different input shapes by copying the text in red in the image captions and pasting it into the data entry window that appears by clicking any of the buttons at the top of the page to perform an operation (Complete study of a function, Study of the domain ,etc…).
To enter a piecewise function, see the 4th example below
Performance of a function study
The softwareperforms the following operations:
-
Calculation of the domain
-
Graph of the domain and the study of the sign of the function in the Cartesian plane
-
Calculation of the intersections with the Cartesian axes
-
Calculation of limits and asymptotes
-
Calculation of the first derivative and its study of sign for the growth and decrescence
-
Calculation of stationary points based on the study of the sign of the first derivative
-
Calculation of stationary points with the method of subsequent derivatives
-
Calculation of non-derivability points
-
Calculation of the second derivative and its study of sign for the concavity and convexity
-
Calculation of inflection points
-
Calculation of the tangents in the inflection points with an oblique tangent
-
Graph of the function both with a panoramic view without necessarily respecting the proportions on the 2 axes and in detail with the points determined in the previous steps
Example of a sign study of the first derivative
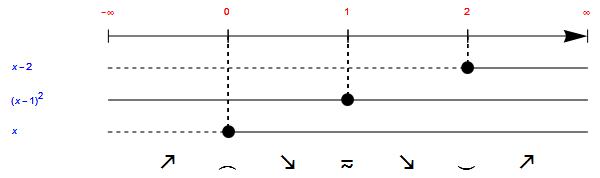
Meaning of symbols:
- Ascending before 0
- Local maximum in 0
- Descending between 0 and 1
- rising point of inflection in 1
- Descending between 1 and 2
- Local minimum in 2
- Ascending after 2
Example of a sign study of the second derivative:
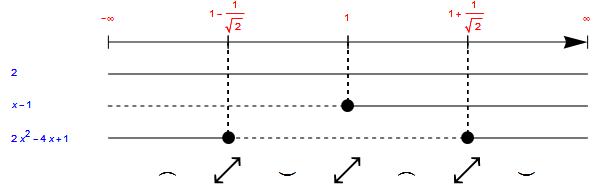
SMeaning of symbols:
- Concave down before 1-1/√2
- Inflection point in 1-1/√2
- Concave up between 1-1/√2 and 1
- Inflection point in 1
- Concave down between 1 and 1+1/√2
- Inflection point in 1+1/√2
- Concave up after 1+1/√2
Note: time limits for performing calculations
The study of particularly complex functions may not be complete. The system is set to reserve a limited amount of time for performing calculations.
In this case you will have one of the following situations:
- the derivative sign studies will be returned in a simplified form: the relative studies of stationary points and inflection points will not return any results;
Example of a simplified sign study:

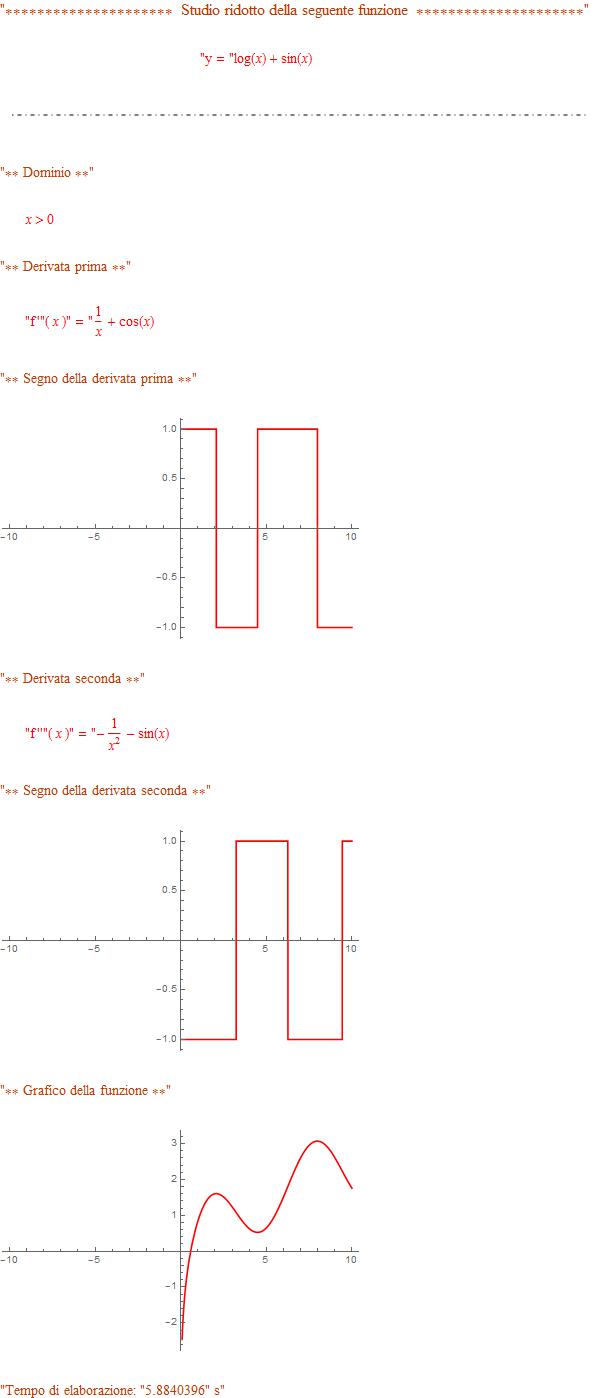
- the entire function study will be returned in a reduced form.
Example of a reduced function study: