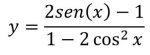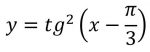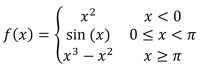Attenzione! Se leggi questo messaggio significa cha hai disabilitato JavaScript
In tal caso le funzionalità del sito non sono disponibili.
Studio di una funzione
Tramite i seguenti pulsanti puoi effettuare lo studio completo di una funzione o avere le singole parti dello studio con maggiori dettagli
Studio completo di una funzione
Studio dettagliato del dominio di una funzione
Studio dettagliato dei punti di discontinuitá di una funzione
Studio dettagliato del segno della derivata prima
Esempi di immissione delle espressioni
Non inserire “y=” ma solamente l’espressione in x
Puoi testare diverse forme di input copiando il testo in rosso nelle didascalie delle immagini e incollarlo nelle finestra di immissione dei dati che compare cliccando uno qualunque dei pulsanti all’inizio della pagina per l’esecuzione di uno studio (Studio Completo, Studio del Dominio,ecc…).
Per inserire una funzione definita per intervalli vedi il 4° esempio quì sotto
Funzione goniometrica fratta (2sin(x)-1)/(1-2cos(x)^2)
Funzione goniometrica intera tan(x-Pi/3)^2
Funzione logaritmica
surd(ln(x);3)
Funzione definita per intervalli x^2,x<0,sin(x),0<=x<Pi,x^3-x^2,x>=Pi
Svolgimento di uno studio di funzione
Il sistema esegue le seguenti operazioni:
-
Calcolo del dominio
-
Grafico del dominio e dello studio del segno della funzione nel piano cartesiano
-
Calcolo delle intersezioni con gli assi cartesiani
-
Calcolo dei limiti e degli asintoti
-
Calcolo della derivata prima e suo studio di segno per la crescenza e decrescenza
-
Calcolo dei punti stazionari basandosi sullo studio del segno ella derivata prima
-
Calcolo dei punti stazionari col metodo delle derivate successive
-
Calcolo dei punti di non derivabilità
-
Calcolo della derivata seconda e suo studio di segno per la concavità e convessità
-
Calcolo dei punti di flesso
-
Calcolo delle tangenti nei punti di flesso a tangente obliqua
-
Grafico della funzione sia con una visione panoramica senza necessariamente rispettare le proporzioni sui 2 assi sia in dettaglio coi punti determinati nei passaggi precedenti
Esempio di studio di segno della derivata prima
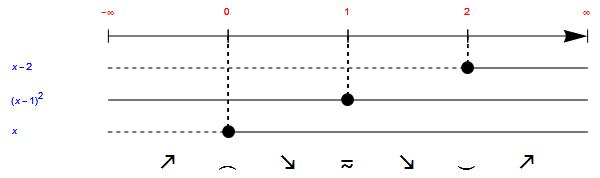
Significato dei simboli:
- Crescente prima di 0
- Massimo relativo in 0
- Decrescente tra 0 e 1
- Flesso a tangente orizzontale discendente in 1
- Decrescente tra 1 e 2
- Minimo relativo in 2
- Crescente dopo 2
Esempio di studio di segno della derivata seconda:
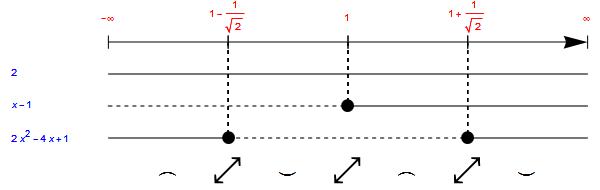
Significato dei simboli:
- Concavità verso il basso prima di 1-1/√2
- Flesso in 1-1/√2
- Concavità verso l’alto tra 1-1/√2 e 1
- Flesso in 1
- Concavità verso il basso tra 1 e 1+1/√2
- Flesso in 1+1/√2
- Concavità verso l’alto dopo 1+1/√2
Nota: limiti di tempo per l’esecuzione dei calcoli
Lo studio di funzioni particolarmente complesse potrebbe non essere effettuato in maniera completa. Il sistema è impostato per riservare un tempo limitato per l’esecuzione dei calcoli.
In questo caso si avrà una delle seguenti situazioni:
- gli studi di segno delle derivate saranno restituiti in forma semplificata: i relativi studi dei punti stazionari e dei punti di flesso non restituiranno nessun risultato;
Esempio di studio di segno semplificato:
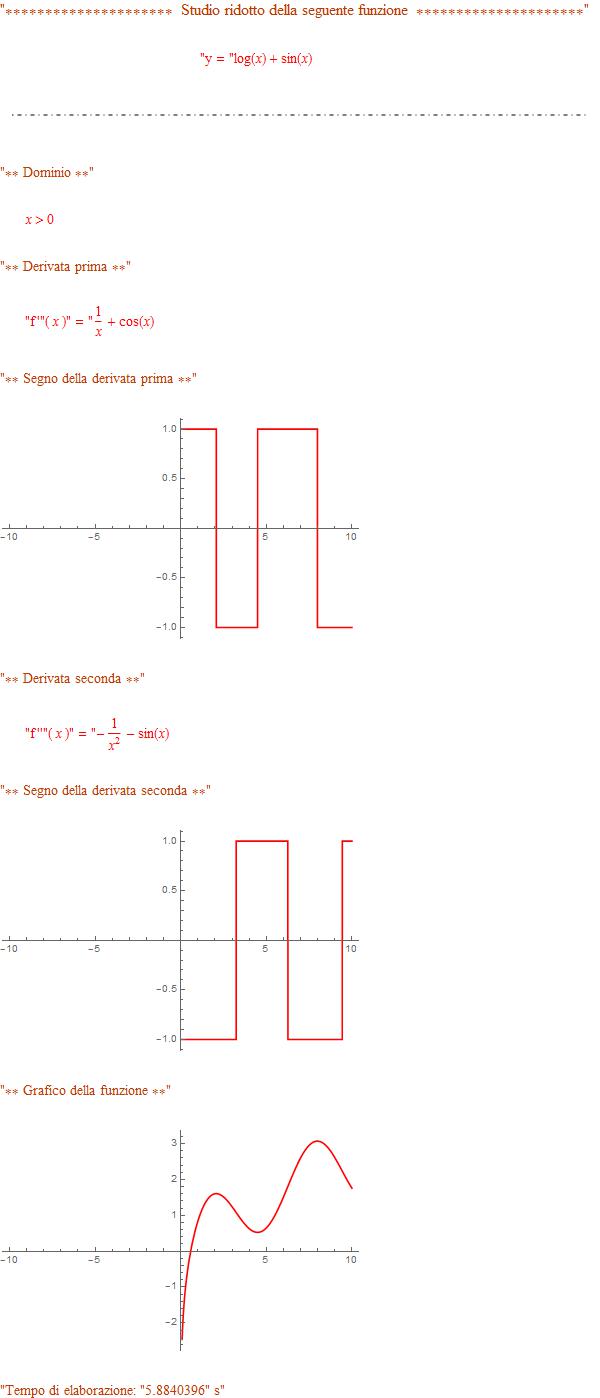
- l’intero studio di funzione verrà restituito in forma ridotta.
Esempio di studio di funzione ridotto:
