Attenzione! Se leggi questo messaggio significa cha hai disabilitato JavaScript

In tal caso le funzionalità del sito non sono disponibili.

 

Math

● Le espressioni si possono inserire solamente tramite la tastiera dell'app
● Il campo nel quale sarà inserita l'espressione è quello evidenziato in giallo
● Il campo in cui inserire l'espressione si seleziona semplicemente facendo click su di esso. Il campo diventerà così evidenziato in giallo
● Non è possibile comporre parole arbitrarie in quanto inserendo le lettere dell'alfabeto verrà inserito uno spazio dopo di essa per cui ogni lettera sarà riconosciuta come una variabile a se
● Inserendo le varie funzioni predefinite verrà inserito il suo nome e quando si cancella questo elemento verrà cancellato l'intero nome

Cancella l'intera espressione

Cancella l'ultima espressione inserita

Sposta il cursosre di un'espressione a sinistra

Sposta il cursosre di un'espressione a destra

Tramite i seguenti pulsanti puoi effettuare le operazioni relative ai punti nel piano cartesiano

Distanza tra 2 Punti
Punto Medio di un segmento
Intersezione di 2 Curve
Baricentro di un triangolo
Circocentro di un triangolo
Ortocentro di un triangolo

Immissione delle espressioni

• Le coordinate dei punti vanno inserite come nel seguente esempio separando le coordinate con la virgola.

sqrt(3),a

• Non c’è bisogno di digitare le parentesi tonde per racchiudere le coordinate
• Le coordinate dei punti possono contenere lettere in quanto viene effettuato anche il calcolo letterale

• Le equazioni (rette e coniche) possono essere inserite sia in forma esplicita che in forma implicita
• Nelle equazioni non si possono inserire parametri quindi devono comparire solamente le lettere x e y
• Il prodotto tra due fattori viene indicato col simbolo * oppure lasciando uno spazio tra i simboli (inserendo una qualunque lettera viene lasciato automaticamente uno spazio dopo la lettera inserita)

ESEMPI DI INPUT E DI SVOLGIMENTI

Puoi testare diverse forme di input copiando il testo in rosso nelle didascalie delle immagini nelle finestre di immissione dei dati che compaiono cliccando uno qualunque dei pulsanti all’inizio della pagina per l’esecuzione di un’operazione (Distanza tra due punti, Punto medio di un segmento,ecc…).

Esempi di Input

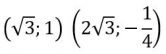
Coordinate di punti sqrt(3),1 2sqrt(3),-1/4

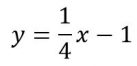
equazione di una retta in forma esplicita y=1/4x-1

Equazione della retta in forma implicita
2x+sqrt(3)y-1=0

Equazione di una conica (completa di secondo grado in x y)
x^2+x y-y^2-x=0

Equazione di una parabola con asse parallelo all’asse x
x=y^2-1

Esempi di svolgimento effettuati dal sistema (fai click sull’immagine per vedere lo svolgimento relativo):

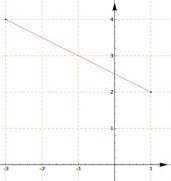
DISTANZA TRA DUE PUNTI: Il sistema utilizza la formula opportuna controllando se i due punti hanno coordinate comuni oppure no.

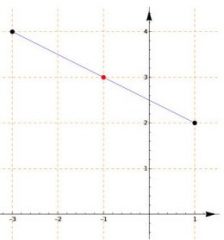
PUNTO MEDIO: il sistema riconosce se i punti hanno qualche coordinata in comune e nel caso adegua l’applicazione delle formule ai dati forniti

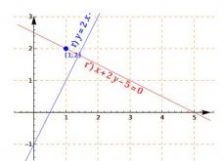
INTERSEZIONE TRA DUE CURVE: Il sistema costruisce e risolve il sistema formato dalle equazioni delle due curve

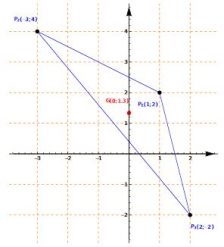
BARICENTRO DI UN TRIANGOLO: Il sistema applica direttamente la formula per determinare il baricentro

CIRCOCENTRO DI UN TRIANGOLO: Il sistema calcola due assi del triangolo e li interseca per trovare il circocentro

ORTOCENTRO DI UN TRIANGOLO: Il sistema calcola due altezze del triangolo e le interseca per trovare l’ortocentro